Et Verkle-træ er en forpligtelsesordning, der fungerer på samme måde som et Merkle-træ, men har meget mindre vidner. Det virker ved at erstatte hasherne i et Merkle-træ med en vektorforpligtelse, som gør bredere forgreningsfaktorer mere effektive.
Tak til Kevaundray Wedderburn for feedback på indlægget.
For detaljer om, hvordan verkle-træer fungerer, se:
Formålet med dette indlæg er at forklare det konkrete layout af udkastet til verkletræet EIP. Det er rettet mod klientudviklere, der ønsker at implementere verkle-træer og leder efter en introduktion, før de dykker dybere ned i EIP.
Verkle træer introducerer en række ændringer i træstrukturen. De væsentligste ændringer er:
Som vektorforpligtelsesskema for verkletræet bruger vi Pedersen-forpligtelser . Pedersens forpligtelser er baseret på elliptiske kurver. For en introduktion til Pedersen-forpligtelser og hvordan man bruger dem som polynomielle eller vektor-forpligtelser ved hjælp af indre produktargumenter, se her.
Kurven vi bruger er Bandersnatch. Denne kurve blev valgt, fordi den er effektiv, og også fordi den vil give effektive SNARK'er i BLS12_381 mulighed for at ræsonnere om verkle-træet i fremtiden. Dette kan være nyttigt til rollups såvel som at tillade en opgradering, hvor alle vidner kan komprimeres til én SNARK, når det bliver praktisk, uden at have behov for en yderligere forpligtelsesopdatering.
Kurverækkefølgen/skalarfeltstørrelsen for bandersnatch er p =1310896879378154761986193512704649145930915589344057025178640330672906817628 , som er en 253 bit prime. Som et resultat af dette kan vi kun sikkert forpligte os til bitstrenge på højst 252 bit, ellers flyder feltet over. Vi valgte en forgreningsfaktor (bredde) på 256 for verkle-træet, hvilket betyder, at hver forpligtelse kan forpligte sig til op til 256 værdier på 252 bit hver (eller for at være præcis, heltal op til p - 1 ). Vi skriver dette som Commit(v₀, v₁, …, v₂₅₅) for at forpligte sig til listen v af længde 256.
Et af designmålene med verkle-træet EIP er at gøre adgang til nabopositioner (f.eks. lager med næsten den samme adresse eller nabokodestykker) billig at få adgang til. For at gøre dette består en nøgle af en stamme på 31 bytes og et suffiks på én byte for i alt 32 bytes. Nøgleskemaet er designet således, at "tætte" lagersteder er kortlagt til samme stamme og et andet suffiks. For detaljer, se venligst EIP-udkastet.
Selve verkle-træet er så sammensat af to typer noder:
Forpligtelsen til en udvidelsesknude er en forpligtelse til en vektor med 4 elementer; de resterende positioner vil være 0. Det er:

C₁ og C₂ er yderligere to forpligtelser, der forpligter sig til alle værdierne med stamme lig med stem . Grunden til, at vi har brug for forpligtelser, er, at værdier har 32 bytes, men vi kan kun gemme 252 bits pr. feltelement. Et enkelt engagement ville således ikke være nok til at opbevare 256 værdier. Så i stedet gemmer C₁ værdierne for suffikset 0 til 127, og C₂ gemmer 128 til 255, hvor værdierne er delt i to for at passe ind i feltstørrelsen (vi kommer til det senere.)
Udvidelsen sammen med forpligtelserne C₁ og C₂ omtales som "udvidelses- og suffikstræ" (forkortet EaS).
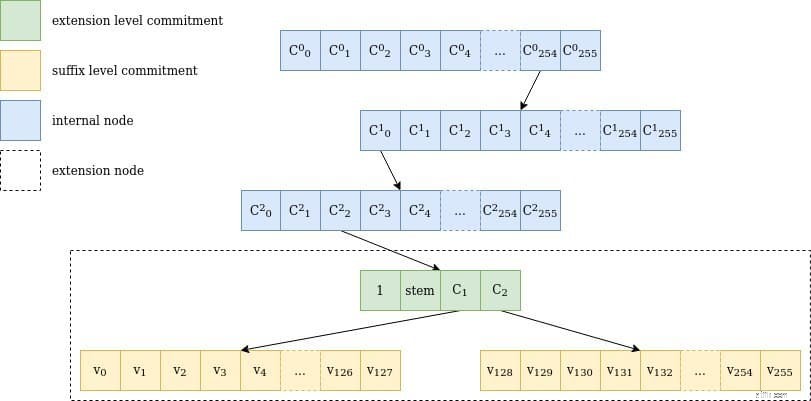 Figur 1 Repræsentation af en gåtur gennem et verkle-træ for nøglen
Figur 1 Repræsentation af en gåtur gennem et verkle-træ for nøglen 0xfe0002abcd..ff04 :stien går gennem 3 interne noder med 256 børn hver (254, 0, 2), en udvidelsesknude repræsenterer abcd..ff og de to suffikstræ-forpligtelser, inklusive værdien for 04 , v4. Bemærk, at stammen er faktisk de første 31 bytes af nøglen, inklusive stien gennem de interne noder.
Hver udvidelses- og suffikstrænode indeholder 256 værdier. Fordi en værdi er 256 bit bred, og vi kun kan gemme 252 bit sikkert i et feltelement, ville fire bit gå tabt, hvis vi blot prøvede at gemme en værdi i et feltelement.
For at omgå dette problem, valgte vi at opdele gruppen med 256 værdier i to grupper på hver 128 værdier. Hver 32-byte værdi i en gruppe er opdelt i to 16-byte værdier. Så en værdi vᵢ∈ 𝔹32 drejes til v⁽ˡᵒʷᵉʳ⁾ᵢ ∈ 𝔹6 og v 𝔹 𝔹6 sådan, at v⁽ˡᵒʷᵉʳ⁾ᵢ ++ v⁽ᵘᵖᵖᵉʳ⁾ᵢ =vᵢ.
En "bladmarkør" føjes til v⁽ˡᵒʷᵉʳ⁾ᵢ for at skelne mellem et blad, der aldrig har været adgang til, og et blad, der er blevet overskrevet med 0'er. Ingen værdi bliver nogensinde slettet fra et verkle-træ . Dette er nødvendigt for kommende statslige udløbsordninger. Denne markør er indstillet til 129th bit, dvs. v⁽ˡᵒʷᵉʳ ᵐᵒᵈⁱᶠⁱᵉᵈ⁾ᵢ =v⁽ˡᵒʷᵉʳ⁾ᵢ + 2¹²⁸, hvis Vᵢ er blevet åbnet før, og v⁽ˡᵒʷᵉʳ ᵐᵒᵈⁱᶠⁱᵉᵈ⁾ᵢ =0, hvis Vᵢ aldrig er blevet tilsluttet.
De to forpligtelser C₁ og C₂ er så defineret som

Forpligtelsen til en udvidelsesknude er sammensat af en "udvidelsesmarkør", som kun er tallet 1, de to undertræ-forpligtelser C₁ og C₂ og stammen af nøglen, der fører til denne udvidelsesknude.

I modsætning til forlængelsesknuder i Merkle-Patricia-træet, som kun indeholder den sektion af nøglen, der bygger bro mellem den overordnede interne knude til den underordnede interne knude, dækker stammen hele nøglen indtil det punkt. Dette skyldes, at verkle-træer er designet med statsløse beviser i tankerne:Hvis der indsættes en ny nøgle, der "deler" udvidelsen i to, behøver den ældre søskende ikke at blive opdateret, hvilket giver mulighed for et mindre bevis.
Interne knudepunkter har den simplere beregningsmetode for deres forpligtelser:knudepunktet ses som en vektor af 256 værdier, som er (feltrepræsentationen af) rodforpligtelsen for hver af deres 256 undertræer. Forpligtelsen for et tomt undertræ er 0. Hvis undertræet ikke er tomt, er forpligtelsen for den interne knude

hvor Cᵢ er børnene af den interne node, og 0 hvis et barn er tomt.
Figur 2 er en illustration af processen med at indsætte en ny værdi i træet, som bliver interessant, når stænglerne støder sammen på flere initiale bytes.
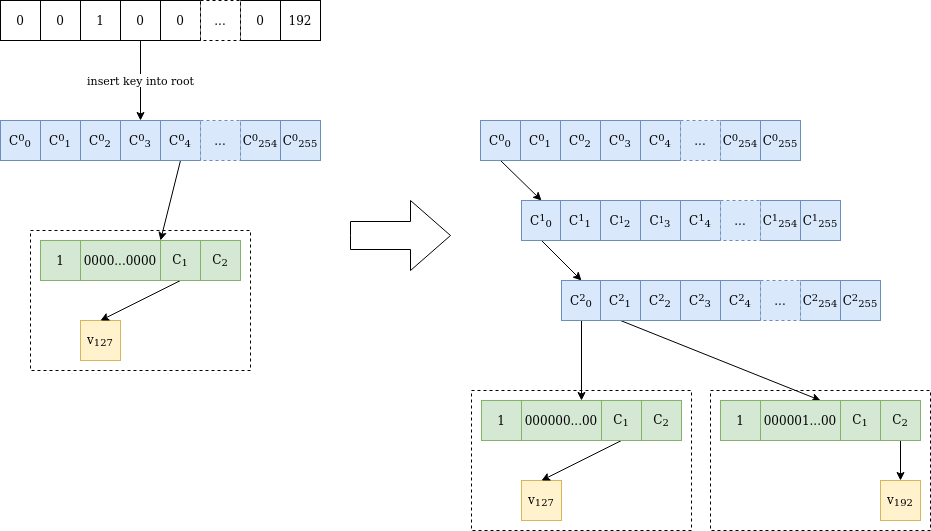
Figur 2 Værdi v₁₉₂ er indsat på lokationen 0000010000...0000 i et verkle-træ, der kun indeholder værdien v₁₂₇ på lokationen 0000000000...0000 . Fordi stammerne adskiller sig ved den tredje byte, tilføjes to interne noder indtil den forskellige byte. Derefter indsættes endnu et "extension-and-suffix"-træ med en fuld 31-byte-stamme. Den indledende node er uberørt, og C²₀ har samme værdi som C⁰₀ før indsættelsen.
Verkle-træstrukturen giver mere lavvandede træer, hvilket reducerer mængden af lagrede data. Dens virkelige kraft kommer imidlertid fra evnen til at frembringe mindre beviser, dvs. vidner. Dette vil blive forklaret i den næste artikel.